1. Description
In 1970s John Horton Conway (British mathematician and University of Cambridge graduate) opened a whole new field of mathematical research by publishing a revolutionary paper on the cellular automaton called the Game of Life. Suffice it to say that the game which he has described with four simple rules has the power of a universal Turing machine, i.e. anything that can be computed algorithmically can be computed within Conway's Game of Life (outlines of a proof for given by Berlekamp et al; implemented by Chapman as a universal register machine within the Game of Life in 2002).

Glider in the Game of Life
- Any live cell with fewer than two live neighbours dies, as if caused by underpopulation.
- Any live cell with more than three live neighbours dies, as if by overcrowding.
- Any live cell with two or three live neighbours lives on to the next generation.
- Any dead cell with exactly three live neighbours becomes a live cell.
For more information, patterns and current news about the research involving Game of Life check out the brilliant LifeWiki at conwaylife.com.
2. Implementation
The following applet visualising the Game of Life has been developed as part of the coursework for Object-Oriented Programming at the University of Cambridge, all code was written and compiled in Sun's Java SE 1.6.
Click on any of the screenshots or the button below to launch the Game of Life (and if nothing shows up, make sure that you have the Java Runtime Environment (JRE) installed).
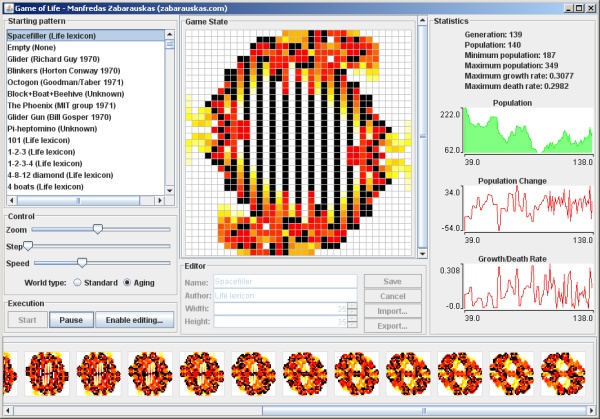
Spacefiller (Game of Life applet)


