The main purpose behind writing this tutorial was to provide a more detailed set of instructions for someone who is trying to implement an eigenface based face detection or recognition systems. It is assumed that the reader is familiar (at least to some extent) with the eigenface technique as described in the original M. Turk and A. Pentland papers (see "References" for more details).
1. Introduction
The idea behind eigenfaces is similar (to a certain extent) to the one behind the periodic signal representation as a sum of simple oscillating functions in a Fourier decomposition. The technique described in this tutorial, as well as in the original papers, also aims to represent a face as a linear composition of the base images (called the eigenfaces).
The recognition/detection process consists of initialization, during which the eigenface basis is established and face classification, during which a new image is projected onto the "face space" and the resulting image is categorized by the weight patterns as a known-face, an unknown-face or a non-face image.
2. Demonstration
To download the software shown in video for 32-bit x86 platform, click here. It was compiled using Microsoft Visual C++ 2008 and uses GSL for Windows.
3. Establishing the Eigenface Basis
First of all, we have to obtain a training set of 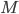 grayscale face images
grayscale face images 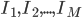 . They should be:
. They should be:
- face-wise aligned, with eyes in the same level and faces of the same scale,
- normalized so that every pixel has a value between 0 and 255 (i.e. one byte per pixel encoding), and
- of the same
 size.
size.
So just capturing everything formally, we want to obtain a set 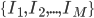 , where \begin{align} I_k = \begin{bmatrix} p_{1,1}^k & p_{1,2}^k & ... & p_{1,N}^k \\ p_{2,1}^k & p_{2,2}^k & ... & p_{2,N}^k \\ \vdots \\ p_{N,1}^k & p_{N,2}^k & ... & p_{N,N}^k \end{bmatrix}_{N \times N} \end{align} and
, where \begin{align} I_k = \begin{bmatrix} p_{1,1}^k & p_{1,2}^k & ... & p_{1,N}^k \\ p_{2,1}^k & p_{2,2}^k & ... & p_{2,N}^k \\ \vdots \\ p_{N,1}^k & p_{N,2}^k & ... & p_{N,N}^k \end{bmatrix}_{N \times N} \end{align} and 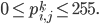
Once we have that, we should change the representation of a face image 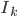 from a
from a  matrix, to a
matrix, to a 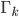 point in
point in 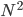 -dimensional space. Now here is how we do it: we concatenate all the rows of the matrix
-dimensional space. Now here is how we do it: we concatenate all the rows of the matrix 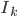 into one big vector of dimension
into one big vector of dimension 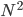 . Can it get any more simpler than that? Continue reading
. Can it get any more simpler than that? Continue reading
