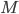During my final year in Cambridge I had the opportunity to work on the project that I wanted to implement for the last three years: a glasses-free 3D display.
1. Introduction
It all started when I saw Johnny Lee's "Head Tracking for Desktop VR Displays using the Wii Remote" project in early 2008 (see below). He cunningly used the infrared camera in the Nintendo Wii's remote and a head mounted sensor bar to track the location of the viewer's head and render view dependent images on the screen. He called it a "portal to the virtual environment".
Johnny Lee's project "Head Tracking for Desktop VR Displays using the Wii Remote".
I always thought that it would be really cool to have this behaviour without having to wear anything on your head (and it was - see the video below!).
My "portal to the virtual environment" which does not require head gear. And it has 3D Tetris!
I am a firm believer in three-dimensional displays, and I am certain that we do not see the widespread adoption of 3D displays simply because of a classic network effect (also know as "chicken-and-egg" problem). The creation and distribution of a three-dimensional content is inevitably much more expensive than a regular, old-school 2D content. If there is no demand (i.e. no one has a 3D display at home/work), then the content providers do not have much of an incentive to bother creating the 3D content. Vice versa, if there is no content then consumers do not see much incentive to invest in (inevitably more expensive) 3D displays.
A "portal to the virtual environment", or as I like to call it, a 2.5D display could effectively solve this. If we could enhance every 2D display to get what you see in Johnny's and my videos (and I mean every: LCD, CRT, you-name-it), then suddenly everyone can consume the 3D content even without having the "fully" 3D display. At that point it starts making sense to mass-create 3D content.
The terms "fully" and 2.5D, however, require a bit of explanation. Continue reading