The PhD thesis of Paul J. Werbos at Harvard in 1974 described backpropagation as a method of teaching feed-forward artificial neural networks (ANNs). In the words of Wikipedia, it lead to a "rennaisance" in the ANN research in 1980s.

As we will see later, it is an extremely straightforward technique, yet most of the tutorials online seem to skip a fair amount of details. Here's a simple (yet still thorough and mathematical) tutorial of how backpropagation works from the ground-up; together with a couple of example applets. Feel free to play with them (and watch the videos) to get a better understanding of the methods described below!

1. Background

To start with, imagine that you have gathered some empirical data relevant to the situation that you are trying to predict - be it fluctuations in the stock market, chances that a tumour is benign, likelihood that the picture that you are seeing is a face or (like in the applets above) the coordinates of red and blue points.

We will call this data training examples and we will describe 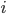$i$^th training example as a tuple 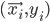$(\vec{x_i}, y_i)$, where 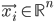$\vec{x_i} \in \mathbb{R}^n$ is a vector of inputs and 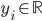$y_i \in \mathbb{R}$ is the observed output.

Ideally, our neural network should output 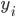$y_i$ when given 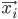$\vec{x_i}$ as an input. In case that does not always happen, let's define the error measure as a simple squared distance between the actual observed output and the prediction of the neural network: 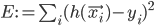$E := \sum_i (h(\vec{x_i}) - y_i)^2$, where 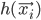$h(\vec{x_i})$ is the output of the network.

2. Perceptrons (building-blocks)

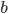The simplest classifiers out of which we will build our neural network are perceptrons (fancy name thanks to Frank Rosenblatt). In reality, a perceptron is a plain-vanilla linear classifier which takes a number of inputs $a_1, ..., a_n$, scales them using some weights $w_1, ..., w_n$, adds them all up (together with some bias $b$) and feeds everything through an activation function $\sigma \in \mathbb{R} \rightarrow \mathbb{R}$.

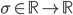A picture is worth a thousand equations:

Perceptron (linear classifier)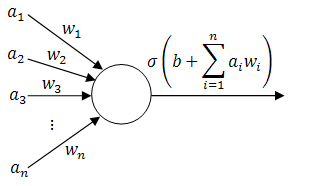

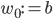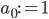To slightly simplify the equations, define $w_0 := b$ and $a_0 := 1$. Then the behaviour of the perceptron can be described as 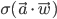$\sigma(\vec{a} \cdot \vec{w})$, where 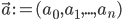$\vec{a} := (a_0, a_1, ..., a_n)$ and $\vec{w} := (w_0, w_1, ..., w_n)$.

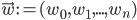To complete our definition, here are a few examples of typical activation functions:

• sigmoid: $\sigma(x) = \frac{1}{1 + \exp(-x)}$,
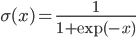• hyperbolic tangent: $\sigma(x) = \tanh(x)$,
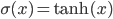• plain linear 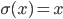$\sigma(x) = x$ and so on.

Now we can finally start building neural networks. Continue reading →