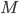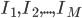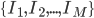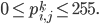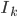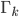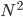... otherwise known as Part 1A of Computer Science Tripos in University of Cambridge has officially ended.
All in all, a rather enjoyable year. From the introduction to ML by the brilliant Prof. Larry Paulson, to the realms of Discrete Mathematics II (with a wicked a proof of existance of ordinal numbers in the exam); from Algorithms to Software Design, from Digital Electronics to Operating Systems, from Floating-Point Computation to Regular Languages and Finite Automata; and everything in between.
A crash course, but the one that is definitely worth going through.
If you're just about to come to Cambridge (or just starting your part 1A), here are a few simple tips that proved to be helpful for me:
- Don't fall behind - in lectures, ticks, homeworks, supervision assignments - in Cambridge pace it's difficult to catch up.
- Do things in advance - it's usually a very good idea and pays off well.
- Make sure that you keep your work/life balance: do a bit of sports (many choices in University of Cambridge Societies website) and go out once in a while. Paradoxically, having a few hours off in a week will help you to stay on top of things.
- Finally, keep an eye on these subjects: Discrete Mathematics II, Operating Systems II, Floating-Point Computation, HW ticks (sorted by the effort they took from me, in decreasing order). They might be different for you, but these particular ones are worth being aware of.
But most importantly - enjoy what you're doing.
Good luck and have fun.